Раздел IX. Сведения по теплотехнике (А. В. Федоров, И. С. Коган)

Теплопередача (основные расчетные формулы)

Уравнение теплопроводности для установившегося теплового потока через однослойную плоскую стенку (ккал/ч; в системе СИ - Вт)

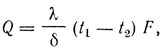
где t₁ и t₂ - температура поверхности стенки, °С;

F - площадь поверхности стенки, м²;

λ - коэффициент теплопроводности, ккал/(м·ч·°С) [в СИ - BT/(M·K)];

δ - толщина стенки, м.

Для цилиндрической стенки

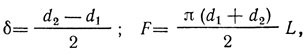
где L - длина цилиндра, м;

d₁ - внутренний диаметр цилиндра, м;

d₂ - наружный диаметр цилиндра, м;

или

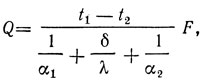
где α1 - коэффициент теплоотдачи от первой среды к стенке, ккал/(м²·ч·°С) [в СИ - Вт/(м²·К)];

α² - коэффициент теплоотдачи от стенки ко второй среде,

ккал/(м²·ч·°С) [в СИ - Вт/(м²·К)];

Общее термическое сопротивление (в м²·ч·°С/ккал, в СИ - м²·с·К/Дж) для однослойной стенки

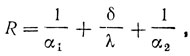
для многослойной стенки

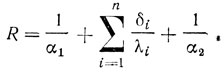
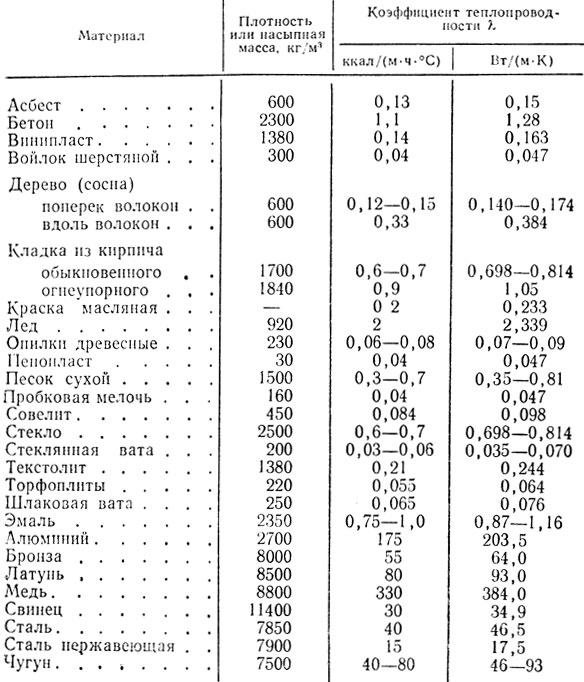
Таблица 157. Коэффициенты теплопроводности некоторых твердых материалов при 0-100°С

Величина k = 1/R называется коэффициентом теплопередачи; размерность коэффициента - ккал/(м²·ч·°С) [в СИ - Вт/(м²·К)].

Расход тепла через стенку (ккал/ч, в СИ - Вт)

Температуру наружной и внутренней поверхности стенки, а также в точке соприкосновения слоев (например, изоляция и стенки) определяют из уравнения теплового потока

где q - удельный тепловой поток, ккал/(м²·ч) [в СИ - Вт/м²)];

Δt₁ - перепад температур от теплоносителя к стенке;

Δt₂, Δt₃ - перепад температур через слои стенки толщиной δ₁ и δ₂,

Δt_n - перепад температур с другой стороны стенки.

Конвективный перенос тепла между стенкой и теплоносителем определяется уравнением (ккал/ч; в СИ - Вт)

где α - коэффициент теплоотдачи, характеризующий количество тепла, которое передается от стенки поверхностью в 1 м² к теплоносителю в течение одного часа при разности температур в один градус, ккал/(м²·ч·°С) [в СИ - Вт/(м²·К)];

t_c - температура стенки, °С;

t_ж - средняя температура жидкости (газа), °С.

Определение коэффициента теплоотдачи а производится с помощью уравнений, полученных на основе экспериментальных исследований с последующей обработкой опытных данных с помощью теории подобия.